Kriptografi Berbasis “Chaos"

Kriptografi Berbasis “Chaos"

Properti chaos yang paling bernilai bagi kriptografi adalah kepekaannya pada nilai awal.  Sebagaimana dijelaskan oleh Schneier (1996), salah satu dari dua prinsip Shannon yang dijadikan panduan dalam perancangan algoritma kriptografi adalah difusi (diffusion), yaitu menyebar pengaruh 1 bit (atau digit) data (plainteks atau kunci) ke seluruh bit cipherteks dengan maksud untuk menyembunyikan hubungan statistik antara plainteks dan cipherteks.  Prinsip difusi ini relevan dengan properti  chaos di atas, sebab jika nilai awal yang digunakan untuk membangkitkan nilai acak diubah sedikit, misalnya 1 bit, lalu nilai-nilai acak itu digunakan untuk mengenkripsi plainteks, maka cipherteks yang dihasilkan akan berbeda secara signifikan. Sifat peka menjamin bahwa jika pihak lawan mencoba mendekripsi data dengan kondisi awal berbeda dan mencari pola hubungan plainteks dan cipherteks, cara itu akan gagal (Roskin, 1999).

Pada dasarnya, terdapat dua cara umum untuk merancang algoritma kriptografi dengan chaos (Li, 2003):

1. Menggunakan chaos untuk membangkitkan barisan kunci bilangan acak, yang digunakan untuk me-“mask” plainteks. Cara ini berkoresponden dengan  stream cipher
2. Menggunakan plainteks dan/atau kunci rahasia sebagai kondisi awal dan/atau parameter kendali, dengan mengiterasikan sistem chaos sejumlah kali untuk memperoleh cipherteks. Cara ini berkoresponden dengan block cipher.

Kebanyakan stream cipher menggunakan pembangkit bilangan acak untuk menghasilkan keystream.  Pembangkit bilangan acak terdapat pada dua sisi, sisi pengirim dan sisi penerima. Dalam hal ini,  chaos dapat digunakan untuk membangkitkan keystream, selanjutnya kesytream ini digunakan untuk me-“mask” plainteks.

 Rancangan Algoritma Stream Cipher dengan Chaos

Algoritma stream cipher yang dibahas  di dalam tulisan ini me-mask karakter-karakter plainteks p_i dengan kesystream k_i yang dibangkitkan dari sistem. Algoritma stream cipher yang dirancang terdiri atas beberapa bagian:

i)  Fungsi pemotongan
ii) Pembangkitan keystream dengan chaos
iii) Enkripsi plainteks dengan kunci
iv) Dekripsi cipherteks dengan kunci

Setiap bagian yang disebutkan di atas dijelaskan secara rinci atu per satu di bawah ini.

 (i) Fungsi Pemotongan

Enkripsi dan dekripsi beroperasi dalam himpunan bilangan bulat yang nilainya dari 0 sampai 255, sedangkan barisan nilai chaos yang digunakan sebagai kesytream adalah bilangan riil antara 0 dan 1. Agar barisan nilai chaos dapat dipakai untuk enkripsi dan dekripsi, maka nilai chaos harus dikonversi ke nilai integer. Ada beberapa teknik konversi yang dapat digunakan, teknik yang umum misalnya mengambil 3 angka terakhir pada bagian mantissa bilangan riil. Sebagai contoh, dari 0.024568 diambil 3 angka terakhir dari bagian mantissanya yaitu 568.

Di dalam tulisan ini, konversi nilai chaos ke integer dilakukan dengan menggunakan fungsi pemotongan yang diusulkan oleh Lampton (xxxx). Caranya, nilai chaos dikalikan dengan 10 berulangkali sampai ia mencapai panjang angka (size) yang diinginkan, lalu memotong hasil perkalian tersebut untuk mengambil bagian integer-nya saja. Secara matematis, nilai chaos x dikonversi ke  integer dengan menggunakan persamaan berikut:

yang dalam hal ini count mulai dari 1 dan bertambah 1 sampai x * 10^count > 10^{size – 1} . Hasilnya kemudian diambil bagian integer saja (dilambangkan dengan pasangan garis ganda pada persamaan 11). Sebagai contoh, misalkan x = 0.003176501 dan size = 4, maka dimulai dari count = 1 sampai count = 6 diperoleh

0.003176501 * 10⁶ = 3176.501 > 10³

kemudian ambil bagian integer-nya dengan

 

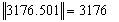
Jadi, diperoleh sebuah elemen dari barisan kunci yaitu 3176. Cara yang sama dilakukan untuk nilai-nilai chaos lainnya. Algoritma konversi nilai chaos ke integer dinyatakan dengan kode program C berikut ini:

(ii) Pembangkitan keystream dengan chaos

Kunci yang digunakan untuk me-mask plainteks dihasilkan dari konversi nilai chaos ke integer, seperti yang sudah diterangkan di atas. Nilai-nilai chaos dibangkitkan dari persamaan Logistic Map dengan mengambil konstanta r = 4.0. Normalnya, nilai x_i dihitung langsung dari nilai chaos sebelumnya, x_{i – 1}. Ini berarti bila seseorang mengetahui sebuah nilai x_i dari barisan nilai chaos, maka ia dapat menggunakan x_i untuk membangkitkan x_{i + 1}, x_{i + 2}, …, yang selanjutnya digunakan untuk mendekripsi cipherteks.

Untuk menambah kekuatan algoritma, maka nilai x_i dibangkitkan setelah sejumlah iterasi tertentu. Tujuannya adalah untuk menghilangkan korelasi antara nilai-nilai chaos yang berturutan. Jumlah iterasi yang dibutuhkan untuk menghitung nilai chaos pertama, x₁, ditentukan oleh nilai awal, x₀. Nilai awal ini dikonversi ke integer dengan algoritma yang sudah dijelaskan di atas, hasilnya adalah jumlah iterasi yang diperlukan untuk mengiterasi persamaan Logistic Map. Nilai x yang diperoleh pada akhir iterasi berlaku sebagai “x₀” yang baru untuk menghitung x₁. Untuk x₂, x₃, dan seterusnya, jumlah iterasinya ditentukan dari jumlah iterasi untuk nilai chaos sebelumnya ditambah dengan size.

Dengan cara ini, seseorang yang mengetahui suatu nilai x_i tertentu tidak mungkin dapat menghitung x_{i + 1} tanpa mengetahui jumlah iterasi yang diperlukan untuk mengiterasi persamaan (8).  Jumlah iterasi awal ditentukan oleh x₀. Jadi, nilai awal merupakan nilai yang sangat menentukan keamanan stream cipher. Terdapat sejumlah tidak berhingga nilai-nilai antara 0 dan 1, oleh karena itu exhaustive key search untuk menemukan x₀ menjadi sesuatu yang tidak mungkin dilalukan. Selain itu, seperti yang sudah dijelaskan di bagian 6, fungsi chaos peka terhadap perubahan kecil pada nilai awal, sehingga jika nilai awal yang dicoba pihak lawan sangat dekat dengan nilai awal yang digunakan untuk mengenkripsi data, pihak lawan masih akan memperoleh keluaran yang salah.

(iii)  Enkripsi plainteks dengan kunci

Enkripsi dikerjakan dengan menjumlahkan plainteks p_i dan k_i dalam modulo 256, seperti yang dituliskan dalam persamaan berikut:

        c_i = (p_i + k_i) mod 256

Alasan pemilihan modulus 256 karena stream cipher mengenkripsi plainteks menjadi chiperteks satu karakter (1 byte) setiap kali.

(iv)  Dekripsi cipherteks dengan kunci

Dekripsi dikerjakan dengan mengurangkan cipherteks c_i dengan pad k_i dalam modulo 256, seperti yang dituliskan dalam persamaan berikut:

        p_i = (c_i – k_i) mod 256

Contoh Enkripsi/Dekripsi Sederhana

Penulis mengilustrasikan contoh enkripsi dan dekripsi sederhana dengan program stream cipher yang sudah dibuat. Nilai awal yang digunakan untuk pembangkitan aliran kunci adalah 0.021503. Plainteks yang akan dienkripsi adalah string “selamat pagi”. Nilai ASCII yang berasosiasi dengan plainteks tersebut adalah

{115, 101, 108, 97, 109, 97, 116, 32, 112, 97, 103, 105}

yang dalam hal ini setiap karakter diepresentasikan dengan angka, misalnya 115 untuk ‘s’, 105 untuk ‘e’, dan seterusnya. String terebut disimpan di dalam berkas plainteks dan cipherteksnya disimpan di dalam berkas cipherteks.  Keystream yang dibangkitkan dengan Logistic Map misalkan adalah

{644, 296, 453, 376, 711, 929, 877, 659, 368, 865, 843, 286}

Kunci ini diperoleh dengan membangkitkan bilangan tiga-angka dari nilai-nilai chaos yang dihasilkan.  Selanjutnya, enkripsi dilakukan dengan cara menjumlahkan plainteks dengan kunci dalam modulo 256. Operasi ini diperlihatkan sebagai berikut:

Perhatikan bahwa semua karakter cipherteks adalah acak (semuanya berbeda) karena kita menjumlahkan barisan nilai acak (kunci) dengan barisan nilai tidak acak (plainteks). Selain itu, karakter plainteks yang sama tidak selalu menghasilkan karakter cipherteks yang sama pula (misalnya 97 tidak selalu menghasilkan 217, tetapi untuk 97 yang kedua menghasilkan 2, sedangkan 97 yang ketiga menghasilkan 194).

Penerima pesan membangkitkan kembali barisan kunci dengan menggunakan nilai awal chaos yang sama, lalu mengurangkan barisan cipherteks (setelah ditambah dengan 256 sejumlah kali sampai nilainya lebih besar dari elemen kunci)  dengan barisan kunci untuk memperoleh kembali plainteks semula:

Hasil-hasil  Eksperimen

Program stream cipher berbasis chaos diujicoba dengan sebuah berkas teks  yang berukuran sedang. Plainteks dapat dilihat di bawah ini. Plainteks dienkripsi dengan menggunakan nilai awal r = 4.0, size = 3,  dan x₀ = 0.00230872. Jika cipherteks didekripsi dengan nilai awal yang sama seperti pada waktu enkripsi, plainteks yang dihasilkan tepat sama seperti semula. Namun, jika cipherteks didekripsi dengan nilai awal yang sedikit berbeda, yaitu x₀ = 0.002308716, maka plainteks yang dihasilkan salah karena barisan nilai chaos yang dihasilkan berbeda (peka terhadap perubahan kecil pada nilai awal).

———— Plainteks ————————————————————————————————————

Seorang wartawan mewawancarai seorang petani untuk mengetahui rahasia di balik buah jagungnya yang selama bertahun-tahun selalu berhasil memenangkan kontes perlombaan hasil pertanian. Petani itu mengaku ia sama sekali tidak mempunyai rahasia khusus karena ia selalu membagi-bagikan bibit jagung terbaiknya pada tetangga-tetangga di sekitar perkebunannya.

“Mengapa anda membagi-bagikan bibit jagung terbaik itu pada tetangga-tetangga anda? Bukankah mereka mengikuti kontes ini juga setiap tahunnya?” tanya sang wartawan.

 ”Tak tahukah anda?,” jawab petani itu. “Bahwa angin menerbangkan serbuk sari dari bunga-bunga yang masak dan menebarkannya dari satu ladang ke ladang yang lain. Bila tanaman jagung tetangga saya buruk, maka serbuk sari yang ditebarkan ke ladang saya juga buruk. Ini tentu menurunkan kualitas jagung saya. Bila saya ingin mendapatkan hasil jagung yang baik, saya harus menolong tetangga saya mendapatkan jagung yang baik pula.”

Moral cerita ini: Begitu pula dengan hidup kita. Mereka yang ingin meraih keberhasilan harus menolong tetangganya menjadi berhasil pula. Mereka yang menginginkan hidup dengan baik harus menolong tetangganya hidup dengan baik pula. Nilai dari hidup kita diukur dari kehidupan-kehidupan yang disentuhnya.

——– Cipherteks ————————————————————————————————————

Ì~Rd+ <‚­ € ¥ÃE£‰nê 8äHX¾¢ˆDWƒÌJ·WK¼ Ox絘 :>czPµ?H CÆtîÌ á¬Bw§îk~>è 0žJ’› Sk¾ &á*Ó5ÅT¢–´} 78£/ùüâÖ9m‚ ºO ¼ 4¶c,>\t&>ëÿÀ: ™ Füt }L˜LüU Ê!Ñ9ÛÌιRds±ùDDÐ×S’ˆOCð¸·F wý¬ð±Á¬ÄS:  íL¢Îßë‘#ÕGi™Ë~Bñ_ƒß×äÝãI×€PÌI?¿têÌ8Ó“g¹/1”{Zµ÷3„ðë,ÄT;%K˜×ý;’ïGEa÷Nâ(Üb©R L«wMëQ9Ž¶Y¤!ínÿIKOöà @Ò­Iô©„;Šñáoì§ß-“Õ$Ž 5Ÿú÷ø ·!_²wyÕÒ@Ó¯ñJ+ó•OÚ=}™ò¥o[„¢Ò¸ /ì šÞ¬EÛçWQ5I (õ ª¼\D?@ýΆ$ëä;™öÕ ô^¤iú|C±ê·@%é6|ÂX%"<TÀÉÒ·[óG<KpÈîŒF #ìÄÞ>rŒ‰*&)bâï[1]ô sä?5_цMM!àç8HÏê±O1Am ~“ØCEü‹÷KuÙ!î[Ê‘Q (5Gž!¨VêSß_ QµíFZRF ë!ËU ’ LÈ®?2Ë öÑÌfI’?ùçzÙí9OòªŽEΠ܀Øð « ,>i¦»„OÊ1[1]\#çÍ V@‹Ë`Ðï7ñ›ÜÛÅ 6ŽZ8ð Ü÷71Ü,›äòN€¿JÐ:ž\C À!»Ig)ŠÒ61 ö ˆ<+ÝÞސ±Ç šEHK=¢‹ &× ¬ø‰¹w>˜9 uï$SºË”àŠh åù4ÚL­ “°÷PN×Æ,s=<þ>š¿·’U€5 ­ùùó >”®G ›¾•ÊÛQƾCàsÉNj F&Iƒv¼#eû ÄŠÝðÝYKèö ;<*ÄLSÉ£H$Ø CGé‑¸. ·òçèþC7§Ì$ä…H WM­k…ô;3ò˜˜k:Dåý× û­-  ¦í8_XÔäÞ¼päW¸(Pö‘Q =ƒÞ5ÚŪ’wæË•ÙGõêÏè8‹-KátG­ð­þ%[1]•0e+ÈWñÔ¿jX$r‚ePbLõ1­ß Þp¶UE ð/’þ}Õ%.0ôWó¡ àV ‹1ì EÝ.“óÂ8/gõ„|?•…J Íò_[î ±ê;·Õ—ÿR‰§Hлzìëz ª½Yƒ¶íï}­£±sVŒkÑöÞ76]_þÞT-жáÜV¦ófOKs¹_Ñbù7› aÉú§¼G1{sZÛFmÃ]ì`Åÿíám»[1]=ŠðØE Ž­rýWîJïHN íÊ& L¾OÌVš ’ À]×zrO6¢F3Í] ÓõÜÍ䞃gp½{¶3pS5TŸFôP’غ ïõÏ Þ-|Mþ]ÎTxÈpKzd …3B0³`NI é\Kuæ¶ì>rh[1]Õˆ[(8à˜:—š¸«AîmL*"nû?ÚsR êð‘ N·_°à 1Îå@gô.Ꮙõè -YF· 42þn ȧ   ìLúÃ:ÊÄËß÷"å[1]ò|ÿK×0áû§K-=¡Z©3þ–ÊYcn×Õ˜áÕIÌfÛ’ó ­¥à%„ß]T/ul      MšeóÒ

Sumber

 http://catatankriptografi.wordpress.com/2012/05/04/kriptografi-berbasis-chaos-bagian-2/